Statik
Für Durchhänger
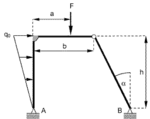
Berechnen Sie den horizontalen Seilzug SH, die maximale Seilkraft Smax sowie die Seillänge L zwischen den Pfeilern der skizzierten Hängebrücke (Spannweite b, Durchhang h).
Unter welchem Winkel α zur Horizontalen läuft das Seil am Pfeiler ein?
Das gewichtslose Seil ist durch die Brückenelemente mit einer konstanten Linienkraft qo belastet.
Das Seil ist an den Pfeilern über eine fixierte Kreisscheibe (Durchmesser D) gelegt; es wird unter dem Winkel β abgespannt.
Wie groß ist die Spannkraft F? Berücksichtigen Sie die Reibung zwischen Scheibe und Seil (Haftreibungskoeffizient μ).
Mit welchem Biegemoment Mz werden beide Pfeiler belastet?
Wie groß müsste der Durchhang mindestens sein, damit die maximale Seilkraft einen Wert von 50kN nicht überschreitet?
b=40 m, h=5 m, qo=1.5 kN/m, β=1.0472 rad, D=0.5 m, μ=0.8
SH=60 kN, Smax=67.1 kN, L=41.61 m, α=0.464 rad, F=20.0 kN, Mz=±11.8 kNm, h=7.5 m
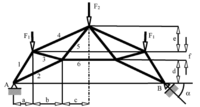
Für Verdrehte
Fd(-1,-3/2,1)
Für Fanatiker
S1=-2.18 kN, S2=-2.18 kN, S3=1.26 kN S4=-2.21 kN, S5=-1.51 kN, S6=0.23 kN
Welche Werte nehmen die Stabkräfte bei einem Winkel α=90° an?
Für Galgenvögel
Für Gespannte
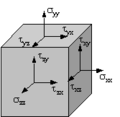
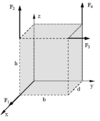
Berechnen Sie die Hauptspannungen im skizzierten Volumenelement eines homogenen, isotropen Materials.
Gegeben sind die Werte zum Spannungstensor im kartesischen Koordinatensystem (x,y,z).
σxx= 50 MPa, σyy= 20 MPa, σzz = -50 MPa
τyx= 10 MPa, τzx= -10 MPa, τzy = 5 MPa
Nutzen Sie die folgende Applikation (Java-Archiv) zum Vergleich mit Ihren Resultaten.