Schwingungen
Für Flatterhafte
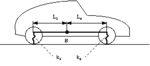
Gesucht sind die Eigenkreisfrequenzen ω1, ω2 von Hub-Nickschwingungen des skizzierten Fahrzeugs mit der Masse m. Das Massenträgheitsmoment der Anordnung bzgl. des Schwerpunkts S hat den Wert ΘS. Das ebene Modell ist über die Radaufhängungen mit den Federkonstanten k1 und k2 elastisch gelagert.
m=1580 kg, L1=1.34 m, k1=29 kN/m, L2=1.71 m, k2=35 kN/m, ΘS=2350 kgm2
ω1=6.04 Hz, ω2=8.35 Hz
Für Hörige
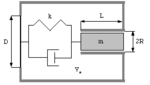
Wie groß ist die untere Grenzfrequenz der skizzierten Bassreflexbox mit dem Boxenvolumen Vo bei einem statischen Luftdruck von 1 bar?
Mechanisch gesehen handelt es sich bei diesem Lautsprechertyp um einen über die Membran erregten, gedämpften Masse-Feder Schwinger (s. Skizze). Die Feder entspricht dem elastischen Luftvolumen innerhalb der Box.
Zur Vermeidung akustischer Kurzschlüsse (Druckausgleich zwischen Vorder- und Rückseite des Lautsprechers) bei tiefen Frequenzen müssen Lautsprechermembran (Durchmesser D) und effektiv bewegte Luftmasse im Bassreflexrohr gegenphasig schwingen.
Das Bassreflexrohr besitzt die Länge L und den Radius R. Luft (Adiabatenexponent 1.4) hat die Dichte ρ.
Vo=20 l, D=110 mm, L=1.7 dm, R=3 cm, ρ=1200 g/m3
f=49 Hz
Für Verdrehte
Berechnen Sie die ersten drei Eigenkreisfrequenzen des skizzierten Biegeschwingers (Länge 2a, Dichte ρ, Elastizitätsmodul E, Querschnittsfläche A, Flächenmoment 2. Ordnung I) mit einem mittig angebrachten singulären Teilkörper (Massenträgheitsmoment J). Der Teilkörper führt Kippschwingungen φ(t)<<π/2 um die Mittellage aus, die über das lokale Biegemoment synchron an die Biegeschwingungen der Stege gekoppelt sind.
a=0.2 mm, ρ=3 mg/mm3, A=100 μm2, E=120 GPa, I=850μm4, J=9.6·10-5 μg mm2
Lösung:
ω1=9.41 MHz, ω2=28.07 MHz, ω3=55.55 MHz
Für Erregte
Welchen Wert hat die niedrigste Erregerkreisfrequenz Ω, bei welcher der skizzierte Biegeträger (Dichte ρ, Elastizitätsmodul E, Querschnittsfläche A, Flächenmoment 2. Ordnung I) in der Wirkungslinie der singulären, harmonisch erregenden Kraft einen Schwingungsknoten aufweist?
Bei welcher Erregerkreisfrequenz tritt erstmalig Resonanz auf?
ρA = 0.96kg/dm, L = 1.5m, EI = 40kNm2
Für Träge
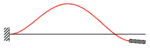
Ermitteln Sie die ersten drei Eigenkreisfrequenzen sowie die zugehörigen Eigenschwingformen eines einseitig fest eingespannten Biegestegs (Länge L, Dichte ρ, Querschnittsfläche A, Elastizitätsmodul E, Flächenmoment 2. Ordnung I) mit einem zusätzlichen, starren Körper (Masse m, Massenträgheitsmoment J) am freien Ende (s. Skizze). Beachten Sie bei den Randbedingungen am freien Ende Querkraft und Moment, hervorgerufen durch die Trägheit des starren Körpers.
L=1 mm, ρ=4 mg/mm3, A=250 μm2, E=100 GPa, I=720μm4, m=20 μg, J=0.4 μg mm2
Lösung (Eigenwerte s. Applikation):
ω1=3.341 kHz, ω2=188.790 kHz, ω3=523.472kHz
Welche Grenzwerte der Parameter m und J führen zu den Eigenschwingungen eines 2-seitig fest eingespannten Balkens bzw. eines einseitig fest eingespannten Biegeträgers mit zusätzlichem Loslager am anderen Ende?
Testen Sie dies mit der folgenden Applikation (Java-Archiv).